los humanos no tenían más remedio que echar mano de lo que llevaban encima, su propio cuerpo, para contabilizar e intercambiar productos. Así aparece el pie, casi siempre apoyado sobre la tierra, como unidad de medida útil para medir pequeñas parcelas, del orden de la cantidad de suelo que uno necesita, por ejemplo, para hacerse una choza. Aparece el codo, útil para medir piezas de tela u otros objetos que se pueden colocar a la altura del brazo, en un mostrador o similar.
en cada una de las profesiones, tienen un juego de herramientas básicas que si aplican a los labores de trabajo. los ingenieros químicos usan pipetas graduadas, probetas graduadas, matraces y vasos de precipitados graduados, termómetro entre otros.
Aparece el paso, útil para medir
terrenos más grandes, caminando por las lindes. Para medidas más pequeñas, de objetos delicados, aparece la
palma y, para menores longitudes, el dedo.
Pero hay un dedo más grueso que los demás, el pulgar, el cual puede incluirse en el anterior sistema haciendo
que valga 4/3 de dedo normal. Con ello, el pie puede dividirse por 3 o por 4 según convenga. Y
dividiendo la pulgada en 12 partes, se tiene la línea para medidas muy pequeñas.
Hasta el renacimiento la mayor parte de la información existente sobre metrología se refiere a su aplicación
en las transacciones comerciales y en las exacciones de impuestos. Solo a partir del Renacimiento se hace
visible la distinción entre metrología científica y otras actividades metrológicas, que podríamos denominar
“de aplicación”.
Es reconocida la relevancia de la metrología en la vida económica medieval y moderna. La burguesía mercantil ayudó a la difusión de los avances a los que asistía la sociedad del momento, progreso impensable sin el triunfo del espíritu de cálculo que originó nuevas formas de vida caracterizadas por lo cuantificable y lo calculable (cf. Flórez Miguel 2001: 28)3 .
.Una regla general observada a lo largo de la historia es que cuanto más barato es un género, más deprisa se
hace su medición y con menor precisión. Hoy día diríamos que tanto la técnica de medición como el
instrumento deben adaptarse a la tolerancia de medida que deseamos comprobar y que, en efecto, mayores
tolerancias permiten una medición más rápida y menos cuidada.
Un hecho que parece claro es el de la aceptación del nacimiento de la ciencia, entendida en el mismo sentido 
que hoy día, en la ciudad griega de Mileto, en el siglo VI a.C. y, posteriormente, en la Alejandría de los
Ptolomeos, hacia el año 250 a.C., nacida de una necesidad puramente práctica. La medición de largas
distancias, basándose en la semejanza de triángulos, según Tales, ha permitido el levantamiento de planos por
triangulación hasta nuestros días.
Son innumerables los ejemplos de la aportación griega a la historia del pensamiento científico y de la
metrología en particular, no solo debidos a ellos mismos sino al rescate de conocimientos anteriores derivados
de los egipcios, haciendo inteligible lo que hasta entonces era confuso.
Los ingenieros químicos usan pipetas graduadas, probetas graduadas, matraces
y vasos de precipitados graduados, termómetro, entre otros. Los ingenieros
electromecánicos usan voltímetros, perímetros, fuentes calibradas, reglas,
calibradores vernier y micrómetros. Los ingenieros industriales usan
cronómetros, micrómetros, calibradores, reglas, cámaras de televisión, entre
otros.Muchas de éstas herramientas son estándares o de propósito general, y sirven para hacer mediciones básicas. El resultado obtenido del uso de estas herramientas depende de la habilidad y la destreza del operador. Por ejemplo, la precisión obtenida depende de la cantidad de presión aplicada al elemento de medición. De este modo, los trabajadores a través del entrenamiento y la experiencia adquieren el sentido del tacto necesario para aplicarlo apropiadamente a las herramientas.
Desde la antigüedad (ya en Babilonia, Egipto, Judea, Grecia y Roma) el hombre ha manifestado un especial interés por la medición de todo aquello que le rodea: el tiempo, el espacio, la temperatura, la masa, el volumen, la longitud, etc. Esta práctica es la que le ha llevado a desarrollar diferentes sistemas de medidas que le han permitido evaluar y describir el entorno en el que vivía en función de sus necesidades.
La existencia de tan diversa cantidad de sistemas metrológicos generó, hasta la fijación del sistema métrico decimal, cuantiosas dificultades en el desarrollo de las transacciones comerciales. Las equivalencias y los nombres de las unidades de medida solían ser distintos por lo que eran frecuentes las estafas o las equivocaciones en negociaciones entre miembros de comunidades distintas, con lo cual, en cualquier tipo de operación comercial, reinaba un “desorden” constante, por llamarlo de forma eufemística, según Moreu-Rey (1986: 6-7). Además, las diferencias entre las medidas y sus equivalencias se las podían encontrar no sólo los miembros de comunidades distintas sino que incluso se podían dar entre habitantes de un mismo pueblo.
Metrología Legal: esta se relaciona con los requisitos que son técnicos obligatorios, con el fin de garantizar unas medidas correctas en áreas de interés público, como la salud, el comercio, el alcance depende de la nación y sus reglamentaciones las cuales varían de un país a otro.
metrologia industrial: Esta se centra en las mediciones que se realizan en el campo de la producción y el control de calidad, procedimientos de calibración, control del proceso de medición, y la gestión de los equipos de medida , es de anotar que en la metrología industrial la persona que necesite calibrar un equipo de medición lo puede hacer en su país u otro.
Metrología científica: Es la parte de la metrología que se ocupa de los problemas comunes a todas las cuestiones metrológicas, independiente mente de la magnitud de medida
calibración de un instrumento de medición
En resumen, consiste en comprobar las desviaciones de indicación de instrumentos y equipos de medida por comparación con patrones con trazabilidad nacional o internacional.
Mediante los resultados de calibración se puede determinar las correcciones a aplicar en las indicaciones de los instrumentos.
Los resultados de calibración se plasman en un certificado o informe de calibración.
¿QUE ES LA INCERTIDUMBRE?
es una cota superior del valor de la corrección residual de la medida. También puede expresarse como el valor de la semi-amplitud de un intervalo alrededor del valor resultante de la medida, que se entiende como el valor convencionalmente verdadero.En otras palabras, siempre habrá un cierto rango de distribución de error cuando se mide el mismo objetivo varias veces.
¿COMO SE CALCULA?
VERIFICACIÓN DE UN EQUIPO DE MEDICIÓN
La verificación consiste en comparar las medidas proporcionadas por el instrumento con las de un equipo calibrado y de calidad metrológica igual o superior al equipo a verificar, con el fin de confirmar que el equipo mide con un error menor al especificado por el fabricante o menor del requerido para la realización de un determinado trabajo.
Las verificaciones se pueden aplicar a instrumentos de medida susceptibles de ser calibrados que no requieran una gran precisión por utilizarse para comprobar que los productos se encuentran entre unos niveles determinados de calidad o exactitud o que cumplen sobradamente con determinadas especificaciones.
exactitud
La exactitud y la precisión son, junto con la incertidumbre, los conceptos más importantes en metrologia , con significados diferentes y bien definidos, aunque en el lenguaje de calle se utilicen habitualmente como sinónimos. Así pues, una medición puede ser precisa y, al mismo tiempo, inexacta.
ejemplos:
1. Cuatro laboratorios farmac´euticos, que llamaremos A, B, C y D, realizan
5 determinaciones, cada uno de ellos, de una muestra de sangre cuya lectura
real suponemos conocida e igual a 10.00 mil. Las determinaciones obtenidas
por los cuatro laboratorios (en mil.) se recogen en una tabla, donde adem´as
se recogen algunos cálculos realizados con ellos.
2.
| Si tu instrumento mide en "unidades" entonces cualquier valor entre 6½ y 7½ se mide como "7" |  |
PRESIONEN DE UNA MEDICIÓN
se refiere a la dispersión del conjunto de valores obtenidos de mediciones repetidas de una magnitud. Cuanto menor es la dispersión mayor la precisión. Una medida común de la variabilidad es la desviación estándar de las mediciones y la precisión se puede estimar como una función de ella. Es importante resaltar que la automatización de diferentes pruebas o técnicas puede producir un aumento de la precisión. Esto se debe a que con dicha automatización, lo que logramos es una disminución de los errores manuales o su corrección inmediata. No hay que confundir resolución con precisión.
Ejemplos:
1. pongamos los disparos a una diana. La precisión y la exactitud en el disparo tienen que ver con la proximidad de los impacto entre sí (precisión), y con la concentración de los impacto alrededor del centro de la diana (exactitud).
En la figura A, tiene un alto grado de precisión dado que todos los disparos se concentran en un espacio pequeño, y un alto grado de exactitud dado que los disparos se concentran sobre el centro de la diana.
En la figura B, el grado de precisión es similar a la de la figura A. Los disparos están igual de concentrados; la exactitud es menor, dado que los disparos se han desviado a la izquierda y arriba, separándose del centro de la diana.
En la figura C, la precisión es baja como se puede ver por la dispersión de los disparos por toda la diana, pero la exactitud es alta porque los disparos se reparten sobre el centro de la diana.
En la figura D, la distribución de los disparos por una zona amplia denota la falta de precisión, y la desviación a la izquierda del centro de la diana revela la falta de exactitud.
2. Un sistema de medición puede tener cualquier combinación de exactitud y precisión. Por ejemplo, un sistema de medición que mide las tabletas de un medicamento es preciso pero no exacto si mide las mismas tabletas de 200 mg como 205.54 mg, 205.43 mg y 205.03 mg. Las mediciones del sistema de medición están cerca unas de otras y, por lo tanto, son precisas. Pero no están cerca del valor real (200 mg) y, por lo tanto, no son exactas.
Exacto y preciso
Las mediciones están cerca del valor verdadero y cerca unas de otras.
Preciso pero no exacto
Las mediciones están cerca unas de otras pero no del valor verdadero.
Exacto pero no preciso
Las mediciones están cerca del valor verdadero pero no están cerca unas de otras.
Ni exacto ni preciso
ERROR DE MEDICIÓN
Al hacer medidas, las lecturas que se obtienen nunca son exactamente iguales, aun cuando las efectué la misma persona, sobre la misma pieza, con el mismo instrumento, el mismo método y el mismo ambiente.
Los errores de medición afectan a cualquier instrumento de medición y pueden deberse a distintas causas. Las que se pueden de alguna manera prever, calcular, eliminar mediante calibraciones y compensaciones, se denominan deterministas o sistemáticos y se relacionan con la exactitud de las mediciones. Los que no se pueden prever, pues dependen de causas desconocidas, o estocásticas se denominan aleatorios y están relacionados con la precisión del instrumento.
ERROR SISTEMÁTICO
es aquel que se produce de igual modo en todas las mediciones que se realizan de una magnitud. Puede estar originado en un defecto del instrumento, en una particularidad del operador o del proceso de medición, etc. Se contrapone al concepto de error aleatorio.
En investigación clínica, un error sistemático se comete por equivocaciones en el proceso de diagnóstico o en el proceso de selección de pacientes:
- Ámbito de selección (de dónde vienen los pacientes): sesgo de selección .
- Sesgo de diagnóstico
- Presencia de factores de confucion: sesgo de confusión.
ERROR CIRCUNSTANCIAL
Los errores circunstancial, estocásticos, o aleatorios Los errores circunstancial, estocásticos, o aleatorios, no se repiten regularmente de una medición a otra, sino que varían y sus causas se deben a los efectos provocados por las variaciones de presión, humedad, y temperatura del ambiente sobre los instrumentos. Por ejemplo con la temperatura la longitud de una regla puede variar, en una pequeña cantidad.
Los errores sistemáticos Los errores sistemáticos, se dan por una mala calibración en el aparato de medición, defecto del instrumento o por una mala posición del observador al realizar la lectura, también se le conoce como el nombre de error de paralaje.
PARALELAJE
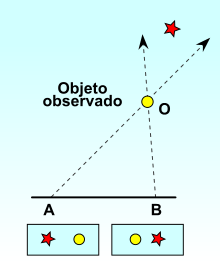
es la desviación angular de la posición aparente de un objeto, dependiendo del punto de vista elegido. Como se muestra la posición del objeto observado, varía con la posición del punto de vista, al proyectar contra un fondo suficientemente distante. Desde el objeto observado parece estar a la derecha de la estrella lejana, mientras que se ve a la izquierda de aquella es el angulo paralelaje : ángulo que abarca el segmento .
ERROR ABSOLUTO
Es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida.COMO SE DETERMINA EL ERROR ABSOLUTO
ERROR RELATIVO
El error relativo de una medida es el cociente entre el error absoluto de la medida y el valor real de ésta.
El error relativo suele expresarse en %.
El cálculo del error relativo en un proceso de medida nos aporta más información que el simple cálculo del error absoluto. Imagina que el error al medir el lado de un azulejo ha sido 2 mm y el error al medir la longitud de una habitación ha sido también 2 mm.
El cálculo del error relativo en un proceso de medida nos aporta más información que el simple cálculo del error absoluto. Imagina que el error al medir el lado de un azulejo ha sido 2 mm y el error al medir la longitud de una habitación ha sido también 2 mm.
COMO SE CALCULA
El error relativo compara el error absoluto con el tamaño del objeto que mediste. Para poder calcular un error relativo, primero debes calcular el error absoluto. Si intentaste medir un objeto de 12 centímetros de largo y tu medida estaba mal por 6 centímetros, el error relativo es enorme. Pero, si intentaste medir algo de 120 metros de largo y solo te equivocaste por 6 centímetros, entonces el error relativo será mucho más pequeño (incluso aunque el valor del error absoluto, 6 centímetros, sea exactamente el mismo).
ERROR PORCENTUAL
es la manifestación de un error relativo en términos porcentuales. En otras palabras, es un error numérico expresado por el valor que arroja un error relativo, posteriormente multiplicado por 100 (Iowa, 2017).
BIBLIOFRAFIAS:
https://www.google.com/search?q=historia+de+la+metrologia&source=lnms&tbm=isch&sa=X&ved=0ahUKEwijrpbetNzfAhVFM6wKHfGSA6gQ_AUIDigB&biw=1366&bih=662#imgrc=b0vbSQBu0GxlAM:
https://magabita.milaulas.com/course/view.php?id=10
https://www.cem.es/sites/default/files/files/breve%20historia_de%20la%20metrologia_doc.pdf
https://www.google.com/search?q=historia+de+la+metrologia&source=lnms&tbm=isch&sa=X&ved=0ahUKEwj087zo0t7fAhUOd6wKHb2kCEUQ_AUIDigB&biw=1366&bih=662#imgrc=n25uf5Kg-MuaeM:
https://es.wikipedia.org/wiki/Precisi%C3%B3n_y_exactitud
https://es.wikipedia.org/wiki/Precisi%C3%B3n_y_exactitud
